(WIP)
Visual intuition from Art of Problem Solving
Idea:
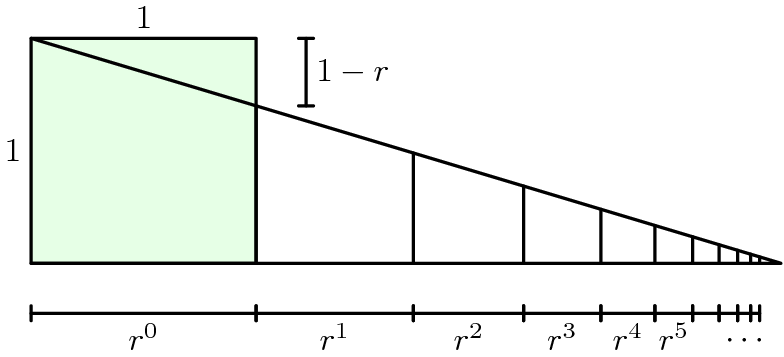
- We have an original element (1)
- We can make a slightly degraded copy (r). Let’s say r = .95 = 95%. Each time we make a copy, we are left with a smaller version. Then a copy of a copy, and so on.
- Keep making copies until we run out of juice
The better our reproduction (95% vs 50%) the longer we can go. 1 / (1 - r). Our fidelity is r, our degradation is 1 - r. For example, 95% fidelity = 5% degradation. We can build 20 full copies before the degradation wipes out our chance to make more.
1 / (1 - r) = 1 / (5%) = 20.
Want a stronger intuition for why here. The key intuition is that the better the fidelity, the more copies. The secondary intuition is why it’s exactly 1 / (1 - r).
From the above diagram: It’s really
$$ \Sigma r^n : 1 = 1 : (1 - r) $$
The ratio of 1 to our degradation is the same as the full amount of copies to 1. Maybe it’s easier flipped:
1 to the amount of copies we get = (1 - r) to 1.
Oh! Here’s a thought. If we have 5% degradation, then after generating 20 copies we must have degraded our full amount (i.e., removed our original copy entirely). You have “diluted out” your original amount entirely. A bit like the puzzle with the fly going back and forth. Instead of adding up the series you just say “we will fly for 1 hour, and it goes 60mph, so the total distance 60 miles.”
Primary intuitions:
- Taxation
- Degredation (fidelity is only r% – how many copies can you make?)