Analogy
-
Quaternions: Logarithm of an orientation
-
Think In Causes: Interest → Growth Rotation → Orientation
-
Interpolate Between Causes: Not effects.
-
Combine Causes: With multiplication
Quaternions: Logarithm of an orientation
Think In Causes: Interest → Growth Rotation → Orientation
Interpolate Between Causes: Not effects.
Combine Causes: With multiplication
Just a placeholder for this topic. Let’s see what happens when we try to expend imaginary numbers to cover 3d rotations.
Use Steve Lehar’s Clifford Algebra as an intro / another way to explain them:
References:
Also: why do we need 4d? Problem of a gimbal lock. When at North Pole, every direction looks South. Need to rotate in 4d space in order to have a smooth (direct) path without some weird jagged motion. (That you might get in 3d software).
Can we create a gimbal lock scenario with our own heads, looking up a certain way?
Euler Angles don’t work the way we need. More advantage/disadvantage discussion: Quaternions and spatial rotation - Wikipedia
http://run.usc.edu/cs520-s12/assign2/p245-shoemake.pdf
euler’s rotation theorem and book example from paper.
4d - vector axis and angle we spin around.
quaternions computationally simpler than 9-element matrix.
"A central message of this paper is that
quaternlon coordinates are best for interpolating
orientations. For comparison, imagine using spherical
coordinates for translations! Quaternions represent
orientation as a single rotation, just as rectangular
coordinates represent position as a single vector.
Translations combine by adding vectors; rotations, by
multiplying quaternions. The separate axes of
translations don’t interact; the axes of rotations must.
Quaternions preserve this interdependence naturally;
Euler’s angle coordinates ignore it. "
euler angles, x-y-z order of rotations matters. quaternions are like a “vector position” for rotation, independent axes taken in any order.
and how do you combine two rotations with euler angles?
quaternions exist in 4d space, do a straight-line interpolation between them. imagine the 4th amount [angle] is a color or similar, interpolate that smoothly as well [same rate of change].
quaternions essentialy define a new axis which represents the rotation and is easy to rotate around. euler angles try to use fixed axis and you try to interpolate 3 simultaneously.
set keyframes for a camera and interpolate smoothly between them in 4d space.
spherical bezier curves. remember the implicit interpolation.
Unity - Scripting API: Quaternion -
“not easy to understand intuitively”, shows core use cases.
Yet another video:
SLERP equation and percentages… see how to intuit that percentage of sine used. what percent of each are we using?
everyone says they are impossible to visualize, unintuitive, etc. think of the path we take as a vector, not a set of rotations. the vector is the axis-independent summary.
one quaternion represents the rotation. multiplying means you are CHANGING the rotation to a new one.
Remember, they aren’t commutative so when you are doing the algebra and switch the order of multiplication, sign reverses.
Argh this makes me want to smash things: Understanding Quaternions | 3D Game Engine Programming
"The imaginary number has the form:
$$i^2$$
Don’t try to actually understand this term as there is no logical reason why it exists. We just have to accept that is just something that squares to ."
See i as a quaternion that rotates around the axis coming out of the paper.
Quaternion is like a “super complex number” where the complex part (a + bi) can be 3 dimensional. It gives you 3 axes to rotate your number around, not just 1 (out of the page).
Video of an apple: iCloud Photo Sharing
Slide 32/100: Each of the rotations can independently find the axis (similar to law of sines, each finding the greater circle). The rotations draw great circles which are parallel to each other. Take the cross product to find the axis they all spin around. (Neat! All the motion is around the same axis). Get angle in radians based on percentage of full circular path it traveled. Get axis, angle representation. Rotate TWICE in order take the cross product and get that axis. Got it. Need 3 points to make a circle: start, position after first rotation, position after next rotation.
Note how Euler angles must be applied in a certain order, prioritizing one axis. Using (x, y, z) to represent orientation makes everything equal. Make vector’s length the angle (i.e. the number of radians we go). Whoa.
Hrm. Does the quaternion HAVE to represent half the angle? Clearly for 90 degree case not necessary. Just use the smaller component and normalize it out.
Another Video: Math for Game Developers - Rotation Quaternions - YouTube
This is like $\cos(\theta) + i \sin(\theta)$ – get two perpendicular vectors (real and imaginary). In the video, they have $\vec{e}$ and $\vec{f}$ . Imagine making a mini axis right there, the e-f axis, and we are picking points on that. Using the standard $\cos(\theta) + i \sin(\theta)$ trick but on the e/f axis.
Realize that a rotation can be represented by 1) the vector you are turning around and 2) the amount you turn. The real part is the amount you turn [scalar] the “imaginary” part is the vector you turn around.
when doing [0, i] we are saying “we are just facing in the i direction, no implied spin yet.” (is this right?)
Axis/angle: $(\theta, \vec{n})$
Quaternion: $w = \cos(\theta/2)$ [so w is the percentage we are using? The /2 is because of two turns to get the plane.], next part is $\vec{n} \sin(\theta/2)$ – axis is scaled (but points same way).
unit quaternion… item on a 4d sphere.
complex number represents a 2d rotation [esp. if normalized, euler’s theorem].
quaternion represents a 3d rotation [and amount].
The quaternion represents the ROTATION we are making but nothing about the object we have. This is the tricky thing, separating the discussion of the rotation from the object which is rotating.
Object has initial orientation and we can describe changes to that.
Identity quaternion is (1, 0) which means… w = 1, which means we haven’t rotated about the axis at all? Which means theta was 0, $\cos(0/2) = \cos(0) = 1$ . We don’t change the axis, just decide not to rotate around it at all.
the notation $q q^{-1} = (1, 0)$ means ‘if we rotate, then rotate again, the result is 0 rotation’ [around an empty axis though?].
to flip the direction of a twist, either flip the vector, or the angle. not both. $(w, v)^{-1} = (-w, v) = (w, -v)$
car wheel axis analogy, spin car around backwards to have axis negative relative to original position.
w is amount of rotation, from -100% to 100%
Key insight from euler: result of ANY number of rotations can be simplified into a SINGLE one. So we can have both effects together [order matters] to get one final result.
Remember, multiplication APPLIES one number to another.
ORDER MATTERS. eat a banana, peel a banana different from peel a banana, eat it.
multiplying quaternions, the new angle: multiply the previous angles, subtract the dot product of the vectors.
Learn to solve rotation problems with complex numbers [as intermediaries]. Then scale it up to quaternions. Get practice with complex numbers first.
OOOH, the point we want to rotate is going to be a quaternion $(0, \vec{p})$ which is really $1 \cdot (0, \vec{p})$ or, we started with 1, and rotated it to BECOME the point we’re interested in. We always start with 1, implicitly!
Rotated point is $p’ = qpq^{-1}$ … and that’s why we have the double angle stuff?
Well, $pqq^{-1}$ have the cancel out, but this isn’t what’s happening. GOTCHA. Remember that order matters. And you rotate halfway, then the rest of the way.
Great analogy with the 4d space and the 1, 2, 3 dimensions otherwise:

Why does the $q q^{-1}$ not bring us back though? Right vs left multiplying? Sort of like the complex conjugate but that will still scale us… left multiply vs. right still works and everything cancels except the rotation?
Walk through actual examples of where you are facing. Quaternion rotations are ABSOLUTE directions [external]. Turn 90 degrees to the left. The x-axis is still facing forward, so when you turn, you start looking up. No gimbal lock problem, you can ALWAYS turn in any direction.
Order matters, where we have q2 * q1 [apply the 2nd rotation to the first]. Implicitly, q2 * q1 * x.
If we want a 90-degree rotation, we need two 45s. So look for .707 as the w value. To actually rotate the vectors you need this (can simplify it for performance):

With quaternions, 1 means no rotation, we still have our original value after multiplying, and 0 means lots of rotation [90 degrees so the value disappears in our dimension!].
GOTCHA: I keep mixing up the angle value we want to rotate and the -1 to 1 value that the w component can take.
That compound rotation [happened in 2 steps] can be done in a single rotation on one axis to get you from looking straight ahead to being tilted left, looking up. Imagine a single head swivel that can point you in that direction.
Think of quaternion as a big bag that represents all the data about the rotation, and we want to interpolate between the bags. These are plotted in a higher dimension. Linear interpolation in that higher dimension.
Algebra of quaternions is different, so need to find the quaternion d which takes us from q [current] to r [desired]. $dq = r$, so $d = rq^{-1}$
We want to scale the quaternion, but can’t change magnitude. Hrm… we are going to scale the ANGLE amount but keep the same direction. That $\frac{\theta}{2}$ portion can be $t\frac{\theta}{2}$.
Becomes exponent… because of Euler’s formula? $d^t q$. Take this and apply a partial rotation to q.
1:33 in this video shows the euler angle dip vs. the quaternion smooth change.
Cool compare/contrast. Quaternions are just for the rotation part of coordinate space.
Quaternions have a 2:1 ness built into them, similar to rational trig.
Rotation problem: how to EFFECTIVELY describe rotations in 3d space. We can have a few systems but they have flaws. Quaternions are great for the pure rotation part.
Also: rotation determined by initial position and final position, don’t think [yet] about intermediates?
Planar rotation can be seen as pair of reflections. !!! Yes, key insight that the rotation we did, we can see it as 2 reflections which are half the size. Oh, hrm, maybe the amount isn’t the same on each… but we have rotation = 2 reflections. Ah. It’s a rotation of twice the wedge angle.
Can compose two rotations [as reflections] into a single rotation. Also though… product of two rotations can be a translation in the planar setting [when they lines are parallel].
Define things in terms of the north/south pole of the axis, even though we turn along the equator. Connect a vector between the north poles of the two planes we are going to reflect through.
IDEA: make a quaternion demo. Let people play and predict. I want to do the rotations in my head. Visualize with Matchbox or three.js etc.
“The quaternions are a number system with a noncommutative multiplication denoted here by *. They can be represented in various ways: as pairs of complex numbers, as four-dimensional vectors with real components, or as the sum of a real scalar and a real three-dimensional vector, as is done in this Demonstration. The scalar part of the quaternion is shown on a line and the vector part is shown in 3D.”
Consider difference between pure i and 1 + i [as a quaternion] where the 1 represents a rotation around the i axis.
Gimbal Lock
When you get to a certain position, you can’t rotate it. Have to tip down in order to spin.
With euler angles you can REPRESENT any position but you can’t easily MOVE between any two positions. (The motion may involve these funky twists in order to “untangle” yourself).
“I should always be able to tilt left”. But when you are at the North pole, you can’t tilt left anymore (with the Gimbal) since both axes point “down”.
Can we simulate gimbal lock for ourselves? Feel it vs. seeing it in an object?
Internal vs. external rotations
In order to prepare for quaternions
“Some coordinate systems in mathematics behave as if there were real gimbals used to measure the angles, notably Euler angles.”
Euler angles behave as IF they were gimbaled.
Show the 2d gimbal lock example. Fly straight overhead, get the telescope aligned upward, then take a sharp right turn. It can’t follow you! (not instantly, anyway). It has to dip down, swivel, then keep tracking. And it has to do this FAST.
Imagine a gunner in a WW2 fighter pilot.
That’s the problem, we have the rotations “internal” to the system and we get trapped here.
Axes move with the object, vs. being universal/external/absolute.
Key problem:
Good explanation of gimbal problem: the telescope

Intuition about rotations:
Euler angles are like being inside with a telescope
Matrix is like having motors on the outside and turning them [rotating]. Intrinsic and external (Rotation matrix - Wikipedia). For x-y-z only that’s 3 external numbers. But… for rotation about an arbitrary axis (a diagonal) then we need a 3x3 or 9-element matrix. Ouch! 9 terms to keep track of.  . Need to specify the axis $(u_x, u_y, u_z)$ and then the amount to turn around it. Still technically 4 unique pieces of data, but “over-specified” in that we need a giant matrix to convert that into rotations for our external motors to do. Under the hood, convert quaternions into this computable format.
. Need to specify the axis $(u_x, u_y, u_z)$ and then the amount to turn around it. Still technically 4 unique pieces of data, but “over-specified” in that we need a giant matrix to convert that into rotations for our external motors to do. Under the hood, convert quaternions into this computable format.
Can we simplify? Yes!
Quaternions is like sticking a pole through an axis and rotating. (axis-angle)
I want to stick a pole through the sphere (x, y, z) and then turn it (scalar).
What does multiplying one quaternion by another do?
It composes the rotations. Similar to multiplying one complex number by another. Get a new number which has both rotations.
Why do we use the $(qv)q^*$? We just want to use v as an axis but not use its actual rotation. So…
$qvq^* = (qv)q^$ which is “compose rotation of v, then rotation of q”. We apply this to $q^$ so we have "compose rotation of $q^*$ with rotation of $v$ then rotation of $q$.
Difference between multiplication (apply i, then apply i again) vs the $qvq^*$ where we are trying to rotate v around q.
Big aha! moment: the quaternion format can be CONVERTED to axis/angle:
http://www.flipcode.com/documents/matrfaq.html#Q47
Quaternions are NOT the same as axis/angle but can be easily converted to them.
Whoa. Remember, sine/cosine trig talk about percentages. Quaternions tell us “What percentage of our original value is remaining after we do a spin around the (x, y, z) axis?)”. We are thinking in terms of results (how much is left) vs the angle itself.
For quaternions, composition (applying one, then the other) is multiplication.
The rotation problem and Hamilton's discovery of quaternions (II) | Famous Math Problems 13b - YouTube starting at 19:00. A quaternion, when applied, will rotate by double its angle. So use half-angled quaternions so the net result works out.
Proof 2 reflections are a rotation. Link 1 And a better one: linear algebra - Composition of two reflections is a rotation - Mathematics Stack Exchange
The rules of quaternion algebra have it so $ij$ will point in the $k$ direction (due to cross products, etc.). Quaternion – ah, multiplying $p$ by $q$ doesn’t necessarily keep length of vector. Multiply by inverse $q^{-1}$ to eliminate scaling factor… but the angles still accumulate. Hrm. That’s the main confusion there.
“The primary diff erence between the two representations is that a quaternion’s axis of rotation is scaled by the sine of the half angle of rotation, and instead of storing the angle in the fourth component of the vector, we store the cosine of the half angle.”
“It means that if you, for example, want to make a 180deg rotation around the Z axis (0,0,1), then the quaternion’s real part will be cos(180deg/2)=0, and its imaginary part will be sin(180deg/2)(0,0,1)=(0,0,1). That’s q=0+0i+0j+1k. 90-degree rotation will give you q=cos(90deg/2)+sin(90deg/2)(0i+0j+1k)=sqrt(2)/2+0i+0j+sqrt(2)/2*k, and so on.”
Complex numbers: we take the idea of $e^{ix} = cos(x) + i*sin(x)$ and have explicit parts. Rotation around an axis.
Quaternions: take the idea of $e^{\vec{u} \theta} = cos(\theta) + sin(\theta) \vec{u}$. Now, usually we want the half quaternions b/c we’ll be applying them twice.
So a 90-degree rotation around (1, 0, 0), i, is really $1/\sqrt(2) + 1/\sqrt(2) * (1, 0, 0)$
Complex numbers and quaternions are different beasts.
Problem with matrices: interpolation. How do you interpolate a rotation matrix? It just shows the final endpoint you’ll be jumped to, but doesn’t have a clear function about where you’ll be halfway through.
Confusion: $i^2 = -1$ for quaternions, yet $i$ represents a 180-degree rotation? Or is it that it’s always a 90-degree rotation (cosine of 0) but when used to convert to axis-angle we have to use that half-angle stuff. i.e., if we used this quaternion in a rotation it would end up being double.
Quaternion multiplication: when we have $ i = 0 + (1, 0, 0)$ times $j = 0 + (1, 0, 0)$, the only interaction that remains is the cross product! I.e., the scalars aren’t there, zero out, and there is no dot product/self-interaction, so we are left with the $i \times j = k$.
Quaternion multiplication: think of successively applying these rotations to the other? Confusion: are we applying rotations in series or saying “all the work that $i$ did, we are going to change it now, like so…”
Thinking about quaternions:
Create a quaternion FAQ:
SLERP vs Euler:
SLERP vs LERP. Rotation matrixes think in terms of (x, y, z) coordinates and take the shortest path between them (a line). Quaternions think with angle/axis so only move via spinning (the white line). We WANT things to move by spinning there, not straight-lining there.
And Euler angles have the weird wobble since they effect each other as they move.
You want a simple interpolation vs. having to re-run the rotation over and over. You have the final position, now find (easily, just by scaling) where the position should be halfway through.
http://unity3d.com/learn/tutorials/modules/intermediate/scripting/quaternions
Gimbal lock - prevents INCREMENTAL rotations from working.
Guide to quaternions
Quaternions let you specify the axis of rotation and the amount to turn around it [from -100% to 100%]. For math reasons, you specify half the amount that is remaining. So if you want to turn 180 degrees around the 1, 2, 3 axis, your quaternion would be
0 + (1, 2, 3)
Learn to go back and forth with the axis/angle and quaternion representation.
SLERP or not… yes, you can interpolate with matrices (opengl - Interpolating between rotation matrices - Stack Overflow) but you are basically re-deriving quaternions to do so. Like staring with decimal, converting to binary, then converting back.
A quaternion represents an orientation: learn to recognize what orientation it’s referring to. i represents a 180-degree orientation, assuming we did i * rotation * i’.
In our head, think “the quaternion we specify is going to be used TWICE”. Imagine two workers. You give them the same command (one is forward turner, one is backward turner). So need to implicitly figure out what to do.
Oh… ok, we have the quaternion (the command we wrote down) and the rotation (the RESULT of the command).
If I see a rotation orientation I like, I can figure out what command would get me there. Imagine two gears and you are putting in the settings for them.
Q: Have to do the conversion between the quaternion and the rotation orientation. This quaternion represents an orientation, just like 0xFF0000 represents red. We want to get comfortable going back and forth.
The quaternion i represents the position after rotating around i twice. Yes, even though i is 90-degrees to the real axis, we aren’t concerned with what happens to a single real number, we want to know how another quaternion (our vector) would be changed. What is happening INSIDE the quaternion bubble?
SLERP equation
$$\text{SLERP}(q_1, q_2) = q_1(q_1^{-1}q_2)^t$$
We start at $q_1$. The term $q_1^{-1}q_2$ represents fully canceling $q_1$ and fully applying $q_2$. We can “partially apply” them using the exponent (again because of Euler’s formula… square root of $i$ is partially applying $i$).
Let’s learn to SLERP in 2d then apply it to 3d after. (Show difference in rotation matrix vs. complex numbers for 2d scenario.)
Analogy: Quaternions are like using binary numbers instead of decimal. Or like using a slide rule to make multiplication easier. (“Quaternions are a rotation-based slide rule.”)
Real part of quaternion is the same when you have qp or pq… only the cross product changes sign:
This can show that qvq* will keep the real part to 0. Therefore v must be rotated and stays unit (just another unit vector). Rotated about the origin somehow.
Imagine twisting up and back down [around the quaternion]. So i [90 degrees] would be 90 + 90 or all the way around when we use it. Twist up, twist down. Imagine the quaternion has an energy meter. We twist until we reach it, then we use q* [opposite twist] and twist it back down again. Want the angle in the real world to be all gone.
The green angle is how much we use in the quaternion world vs. the real world. We can “ease off” the quaternion, so to speak, by only using 10% of the quaternion and the rest in the real world [no rotation]. We have non-rotation and rotation, and we pick how much of each we use [THAT is the real/complex angle] then within the rotation world, we pick the axis we want to use.
In quaternion world, even a single qv multiplication will start giving us the cross product… 2 cross products can rotate use back to start or continue the rotation. Yes, the single multiplication is like the start of the twist.
visualize switching domains : http://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/transforms/derivations/vectors/quaternionReflection.png
http://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/transforms/
Nice description/diagram for Gimbal Lock: http://www.chrobotics.com/library/understanding-euler-angles
Another summary: http://www.geometrictools.com/Documentation/Quaternions.pdf
Complex numbers/quaternions from linear algebra: Complex numbers and Quaternions as Matrices
Suggestion: Humane Rigging 03 - 3D Bouncy Ball 05 - Quaternion Rotation - YouTube
Unity 3D has axes: Y, X, Z … so that is the order you use. You can get gimbal lock based on the internal angles AND the ordering. The ordering is what causes the issue. You get into a position just fine, but transitioning between them is what causes problems.
A quick analogy: Just like logarithms describe “interest rate” behind observed growth, quaternions describe the “twist” behind an orientation. Focusing on the inputs, not the final result (the actual monetary value or actual orientation) makes certain problems easier, especially around interpolation. It’s much easier to “partially apply” a twist than the actual orientation. (Linearly interpolating between final positions doesn’t give the effect we want.)
TODO: work out SLERP formula myself. Be able to compute this by hand as well.
Here’s another potentially useful link: Computer graphics perspective that mentions Lie Group interpretation
Posted this on reddit:
Imagine a biologist notices a bacteria population grow from 100 to 200 in 10 days. We have the data points (0, 100) and (10, 200) and might think we can just smoothly interpolate them. Day 5 must be halfway through at 150, right?
Nope. We know populations grow along an exponential curve. If we want what happened on day 5, we need to reverse out the implicit growth rate [ln(200/100) / 10 = 6.93% continuous growth] and walk that forward: Day 5 is e^{.0693 * 5} = 144.
A straight line interpolation might finish at the same location as the curve (10, 200) but it miscalculates the intermediate positions. It’s not a good model of how bacteria change, we need to find the root input that went into the exponential growth.
Ok. Take this to rotations: at t=0 we start with yaw/pitch/roll of 0/0/0 and at t=10 we’re at some new orientation (45, 90, 180).
Where were we at t=5? Can we just divide each angle by half? Nope! Objects don’t move by interpolating their angles, they rotate along an axis. Interpolating the raw angles on a straight line miscalculates the position just like a straight-line projection miscalculates an exponential curve.
The correct way is to reverse engineer the axis we rotated around (and the angle we passed through) and walk that forward halfway. That’s exactly what quaternions do: they represent the axis + angle that led to the growth (like an interest rate and duration) and they can be smoothly “walked forward” from start to finish.
If you’re just dealing with final results (“200 bacteria” or “45/90/180 orientation”) you don’t need quaternions. But if you plan on changing your orientation, you need them to correctly model the intermediate positions without weird artifacts (like going too fast or too slow).
Working on ways to turn regular exponential growth into rotations with quaternions. There is a lot of overlap there.
Focus on the scenario quaternions enable, not simply their algebraic properties. See how to think with them before you know all the rules.
As a mental check, be able to eyeball a quaternion and see what axis and angle it encodes. The real part is what is visible from the original after the rotation so, use that to reverse out the angle that must have led to that amount being visible.
Intuition for quaternion multiplication: the cross product (different interactions) is good, and the similar interactions hurt us. Add the cross product and subtract the dot product. We can then expand to scalar and vector parts. Quaternion multiplication rule is that we need to account for every similarity (which goes neg and hurts us) and difference.
Intuition for the reason we need 3 coordinates, as lat/long is degenerate at the poles (no unique representation). 2d parameterization can show how (w,x,y) encodes a certain rotation of a/2 around (x,y,0).
Rodriguez formula, the cross product is a 90 degree rotation of the perpendicular component! It works by just rotating the perpendicular portion (the cross product) and we keep the dot. Looking at the quaternion qvq-1 setup we can recognize the pieces.
Separate the key intuition from the algebraic justification. Quaternion help us interpolate. We have to use them twice (to cancel some artifacts) and that’s why we get the half angle.
The algebraic rules of quaternions models 3d rotations, just like the algebraic rules of imaginary numbers models 2 rotations. An “algebra” is a set of behaviors, and we see what scenarios ALSO have these behaviors. Quaternions weren’t invented to solve rotations – they exist on their own. But, it was discovered that their behavior matches up with how rotating objects behave.
Quaternions have certain properties (like negative numbers) and it’s up to us to interpret it as a rotation. Negatives can be interpreted as debt. Quaternions were strange until interpreted as rotations. “The rules for how quaternions work are the same as how rotations work!”
Just like exponential curves model population growth better than lines, quaternions model rotations better than linear interpolations between orientations. Here’s the gotcha: we can interpolate the causes (the interest rate and duration, or the quaternion itself) and then plug into the exponential to find the effects (actual population, final orientation). You don’t want to interpolate between effects.
Imaginary numbers weren’t invented to solve 2d rotation problems. But it turns out their behavior matches exactly, so it can be done. Quaternions weren’t invented to solve 3d rotation problems. But it turns out their behavior matches, so they can be used. In math, we create hypothetical objects that lie dormant for decades or centuries, until someone discovers they exactly correspond to some problem in our world. It’s up to us to find these links.
Explain how to extend Euler’s formula to represent a quaternion. 3d rotation. The real component is how much we still see of the original.
Explain why quaternions are required, they form a division algebra (every operation has an inverse). A good property to have!
Intuitive quaternions for graphics programmers (explain how/why you’d use them, how to think with them), quaternions for math enthusiasts (explain how the rules work, why they work). Have a mathbox demo for them too, to practice your intuition. q= [1, 2, 3, 4] = (w, i, j, k). 4 items we deal with and learn to multiply.
Key insight: the real component of the quaternion is how much we want visible. A pure quaternion like i (0, 1, 0, 0) means that there is nothing visible in the real dimension when we’re done. That is, it’s a full, 90-degree rotation around the axis defined by i. (i-rotation-axis, vs i-dimension).
Why 4 terms? 3 for the axis, 1 for how far to rotate around it (the angle). Q: Could we combine them into the length of the axis angle? Yes, but want unit length on the axis we are rotating around (right?). Hrm.
“If you are just positioning objects, you don’t need quaternions. Use yaw/pitch/roll and go home. But if you need to change orientations, quaternions help you make changes without weird distortions.”
Consider “position quaternions” (0, v) vs. “rotation quaternions” (norm 1). Position quaternions are just meant to be transformed to another position by a rotation quaternion. The qvq* rule means this can happen because we know there is 0 real part in the position. This behavior happens to line up with the rules of rotation.
Quaternions weren’t invented to perform rotations. If you want that, you can use a giant 3x3 matrix with a bunch of trig. Quaternions are a simple structure that, with a little help, can perfectly model rotations. They’re really compact and avoid lots of matrix problems. Quaternions are like q-tips: technically not for your ears, but wow it feels good!
Think of quaternion (s, v) as (percentage visible after rotation, axis of rotation). It’s not quite axis-angle but can be converted pretty easy with some inverse cosine action. We have to remember we’ll be applying the quaternion twice (again, because they were not made for rotations, they just fit the scenario really nicely with a simple modification). Like using Coke to clean your drain. Not its intended use, but it works great. In your head, think: In order to use quaternions for rotations, I need two of them. I’m sticking together a rotation out of these things. Like doing multiplication with logarithms… need a few steps before and after, but it makes the intermediate steps easier!
Key insight: the main reason for this weirdness is because quaternions weren’t made for rotations. It’s a beautiful math hack that we can do a few quaternion operations and sidestep a pile of trig. Like using Euler’s Formula to avoid the trig addition identities.
We can use Euler’s formula for quaternions, but don’t get the exponential add/multiply relationships since ab != ba (http://math.stackexchange.com/questions/41574/can-eulers-identity-be-extended-to-quaternions)
Two quaternions can represent the same rotation: flip both the axis and the angle. u, theta and -u -theta.
Only Reals, Complex and Quaternions are division algebras (http://en.wikipedia.org/wiki/Frobenius_theorem_(real_division_algebras)). If you absolutely want only 3 dimensions, then you can use a 3d rotation matrix. (Enjoy.)
“Multiplying two quaternions is unintuitive, but I’m not
bothered by that, because the composition of two rotations in real life
is quite unintuitive in the first place.” - http://math.stackexchange.com/questions/7187/how-can-one-intuitively-think-about-quaternions - composing rotations [rotating a rotation] is counter-intuitive. Can we understand this?
Complex numbers weren’t invented to solve 2d rotation problems. But it turns out, multiplying by a complex number performs a 2d rotation. Quaternions weren’t invented to solve 3d rotation problems, but multiplication with two quaternions (qvq*) performs a 3d rotation.

is equivalent to the rotation formula. Sort of like using log tables to do multiplication by turning it into addition. Use quaternions to make a 3d rotation into a multiplication problem.
“They were looking for something similar in ℝn for n>2. It turns out that Hamilton spent 13 years in vain with n=3
although it was essentially known since Diophantus that what he was
looking for was impossible. He finally figured out that he could
succeed for n=4 if he gave up commutativity.” 13 years! Wow. http://math.stackexchange.com/questions/911807/what-is-the-motivation-for-quaternions
Another link on quaternions: http://www.optimuscopri.me/quaternions.pdf and proof that {1, i, j} isn’t a field: http://math.stackexchange.com/questions/911720/why-should-i-consider-the-components-j2-and-k2-to-be-1-in-the-search-f
Some want to appreciate quaternions like a fine wine. Others (ahem) want to let the wine sit, modify it a bit, and use it as vinegar. We’ve got cleaning to do! That’s how the quaternions are: they are a beautiful algebraic structure, we can get into all the nuance, but really, some people just want to get that disinfectant. Graphics programmers: “Wine plus baking soda is a good way to get out grease stains. Great!” Mathematicians: “You… you monsters! That’s a 100-year old Chianti”
Quaternion rotation essentially happens in 3d, where you restrict your input to (i, j, k). The 4th dimension is like a “carry” location which is used for intermediate calculations while the quaternions interact. After we’re done, that carry location is back to zero and we’ve rotated as follows: v’ = qvq*.
Complex numbers: notice how we sidestepped the need for trig (see any sines/cosines there?) and rotation matrices. This is something we could even compute by hand. Quaternions are similar: there is no explicit trig (you need enough to know which quaternion should be used, just like knowing “1 + i” would lead to a 45-degree angle. Using (1 + i) in the quaternion case can rotate you 90 degrees around the “i” axis. Go through that example! Idea: have a quaternion parser that shows you what will happen when you do each multiplication and what result you end up with. [In the demo]. Be able to think with it (0, 1, 2, 3) * (0, 1, 2, 3) * (0, 1, 2, 3) etc.
Like the code/data duality. The result of our first rotation is used to spin the original amount (which was a command, now treated as “data”).
Have a FAQ up front:
I hope you like trig, linear algebra, and tears. 4 measly dimensions aren’t looking so bad now, eh?
What do quaternions represent? Nothing. I mean, numbers are abstract concepts that we find uses for. Negatives stumped us (Egad, less than nothing?) until we applied analogies like debt. Quaternions, it turns out, line up really closely to rotations, and can be easily converted to an axis + angle model of rotation. (They aren’t this exactly, but can be converted to it.)
How do you intuitively think about a quaternion? I see a quaternion as representing (percentage, axis). You specify an axis to spin around, and the percentage of the original you want visible. 0% visible means you rotated 90 degrees, and 100% visible means you didn’t rotate at all.
What problems do quaternions avoid? (Gimbal lock, SLERP, numerical precision issues, simpler representation).
If your objects are never change orientation you don’t need quaternions. Good luck with your painting simulator.
A wolfram alpha demo: http://demonstrations.wolfram.com/FromQuaternionTo3DRotation/
Key insight:
Also: practice rotating numbers in 2d with imaginary numbers. 1 + i has a scaling effect. Do (1 + i) / (1 - i) to get back to i. [cancel out magnitude with two half operations].
Note from a reader:
Hi, I read some of your blog posts a while ago and they really helped me understand some aspects of maths better (especially complex numbers, which are really extremely simple in the end). I already have a good mind for mathematics but seeing things explained visually like you do helps a ton.
Earlier this week I watched a video that quickly went over Quaternions, a few of their properties (i^2 = j^2 = k^2 = ijk = -1, and the noncommutative property), and was really left starving for more details. I looked around for something to help me understand them, but never found anything very satisfying, only obscure formulaes and walls of text. So in the end, I decided to make my own visualization and I think it turned out pretty well.
I guess there’s no real point in this message, only to thank you for helping me to the point where I discovered something like this myself. Visualizations like the ones you make, and inspired me to make, are in my opinion the best possible way to learn maths.
Note, using the above you can really visualize what should happen as you rotate. Excellent!
Numberphile video:
Giving some ideas around how to convey these. I would like to show how the nature of rotation can be described by quaternions, not the reverse. (Quaternions weren’t explicitly made to model rotations. They happen to be easily morphed to them.)
Why is it theta/2? Because we intend to do two half-rotations. But that’s only to remove the extra cruft from the multiplication. We can do a single rotation, drop the cruft, and normalize.
Another nice interaction with a world map:
Has 3d rotations, can see the Euler angles and Gimbal lock problems (changing one angle changes the others in a non-predictable way).
Great writeup here:
http://loopspace.mathforge.org/HowDidIDoThat/Codea/Quaternions/#section.1
The problem with most writeups is they have descriptions without visualizations. The eventual article needs a quaternion simulation where we can play with the ideas and try out experiments.
@kalid This writeup worked really well for me:
It goes into Geometric Algebra and explains the basics. The “Scalars and Bivectors” section has some insights that really clicked. Crude summary:
Bivectors are rotations by 90 degrees (like i), we have 3 basis bivectors for 3 planes of 3D rotation
Rotating a vector v is just “mixing” together v and v rotated by 90° (i.e. first scaling both by the right amount, and then normal vector addition). Sounds like complex numbers?
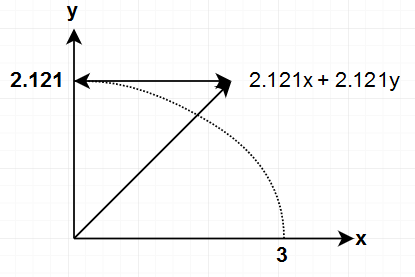
Rotating [3, 0] by 45° (the article has a step-by-step explanation of this image, and many other visual examples!)
To rotate in 3D, we just do the above but with three rotation-by-90° planes instead of one
The post also links to the author’s interactive, WebGL? based tool that lets you visualize this, but I haven’t checked it out yet.
(Also, what shortcode did you use to make those nice link boxes? I tried
[onebox url="https://probablydance.com/2017/08/05/intuitive-quaternions/" title="Less Weird Quaternions"], but it didn’t work.)