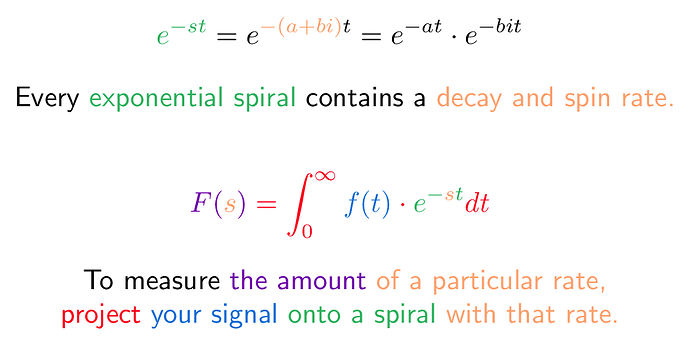Key Intuition
- The Fourier Transform breaks signals into a series of circular components
- The Laplace Transform breaks signals into a series of spiral components
The equation
$$ F(s) = \int_0^\infty f(t) e^{-st},dt $$
Here, s is really the complex number $s = a + bi$ , so we have
$$e^{-st} = e^{-(a+bi)t} = e^{-at} \cdot e^{-bit}$$
where $e^{bit}$ is a pure rotation (from Euler’s formula) and $e^{-at}$ is a diminishing exponential “envelope” that changes the radius. The combination of rotation + changing radius = spiral. The integral above is doing a continuous dot product onto the spiral to measure its strength.
Applications
- The Laplace transform includes a decay factor (negative exponential growth) so is better for real-world engineering, where signals decay. The Fourier Transform has no decay factor and is better for beats in audio signals, etc. (assumed to repeat forever).
Other good resources:
http://bit.ly/kQblzh (good PDF) mp.mathematical physics - Motivating the Laplace transform definition - MathOverflow (discussion) http://bit.ly/mUfozO (great vid)
LaPlace transform but see it as a generalization of the Fourier Transform.
The Fourier transform sees any signal as a sum of cycles or circular paths (see the recent article on the homepage).
The LaPlace transform sees any signal as the sum of spirals, or circles that are growing /shrinking by some factor.
The exponent (s) represents the rate of growth/shrinking in the real part, and the rate of rotation in the imaginary part. When s is purely imaginary, we have no growth or shrinking, and are left with the Fourier transform.
More notes here:
(Quick preview: if the Fourier Transform expresses a signal with circular ingredients, the LaPlace Transform expresses a signal with spiral ingredients. A spiral has both a decay factor and rotation speed, which requires a complex number to represent [the real part, typically negative, is the decay factor, imaginary part is the rotation speed]. So, it’s just another smoothie, but with more complex ingredients.)
To learn:
- Pole diagrams - http://ocw.mit.edu/courses/mathematics/18-03-differential-equations-spring-2010/readings/supp_notes/MIT18_03S10_chapter_22.pdf
- When we do pole/zero diagrams, we are making a 2d plot with a real magnitude (even though the LaPlace transform is actually complex-valued). But we get a surface which might give us an idea of the behavior:
 from Pole/Zero Plots Part 1 - YouTube
from Pole/Zero Plots Part 1 - YouTube
Question: is a zero/pole diagram enough to specify an entire surface?
Notes from an email reply:
The LaPlace transform takes a signal and represents it as a complex surface:
Inline image 1
This representation is actually overspecified, in that it contains way more information than the original. For example, imagine I give you a data point like the number 5. I could do a 1:1 transformation and convert it to binary (101), which is like the Fourier Transform [just enough info to recreate the original signal].
I could go crazy and try to represent the number 5 in every base (unary: 11111, binary: 101, ternary: 12, base4: 11, base5: 10, base6: 05, base7: 05). But instead of giving you the value at every base, I’ll give you a function where you plug in the base and I’ll return the result. (So if you plug in 1, for base 1, it returns 11111. Plug in 2, get 101).
The LaPlace transform is like that: it’s an overdetermined function that can recreate the original signal. Why do we use it? There might be properties about the way this function behaves (where it spikes off to infinity or hits zero) that gives information about the input we’re trying to model. Basically, the presence of poles/zeros in this “super function” might tell us how the number 5 behaves. (That it’s odd, that it’s less than a certain amount, etc.)
I found a good video: Pole/Zero Plots Part 1 - YouTube [2 parts] and it seems that’s the gist: based on the poles/zeros of the LaPlace transform, you can make guesses about the properties of the input signal [that it must have a step function, that it has 2 decaying exponentials, etc].
Idea: Use the new mathbox to create visualizations for the transform. We are putting a function into a higher-dimensional space (in many ways) by making an entire surface, vs a Fourier Transform which is giving us a single slice.
Colorization: