Summary
The imaginary number i represents a rotation into the second dimension (the name “imaginary” was an insult, and it stuck). Negative numbers flip positive numbers 180-degrees, all at once. Imaginary numbers are “half a flip” or a 90-degree rotation.
Analogies
Negative numbers were distrusted until the 1700s: How could you have less than nothing?
We eventually realized numbers could exist on a number line, allowing us to move forward or backward from zero.
Imaginary numbers express the idea that we can move upwards and downwards, or rotate around the number line.
Diagram
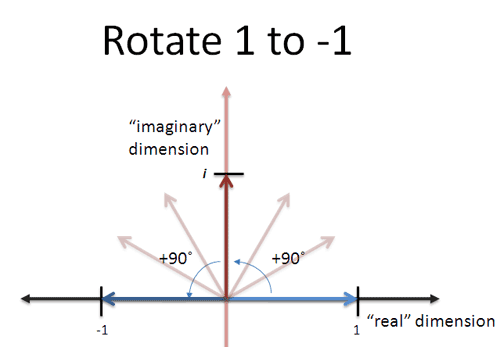
Example
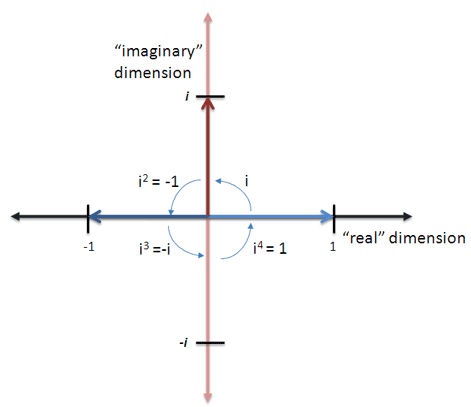
Rotate a number around a circle (two turns is $i^2$, four turns is $i^4$):
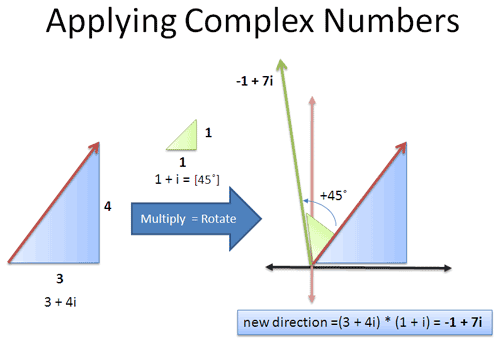
Example
Rotate a vector with imaginary numbers (no trig!):
Technical
- We say $i$ (lowercase) is 1.0 in the imaginary dimension. Adding $i$ moves upward, multiplying by $i$ rotates you.
- Imaginary exponents create a rotating circular path (Euler’s Formula)
- The choice of $+i$ being counterclockwise is arbitrary. Swap $i$ and $-i$ and equations still hold. $i^2 = -1$ becomes $(-i)^2 = -1$. $i^3 = -i$ becomes $(-i)^3 = i$. All are correct.
Resources
Intuitive Guide to Imaginary Numbers
Video: Understanding Imaginary Numbers | BetterExplained
FAQ
I don’t get it. How can $i$ exist? I can’t hold $i$ coins in my hand!
- Well, can you hold -3 coins in your hand? Or $\pi$ coins? Numbers are concepts: negative numbers are the idea of going “backward”, and imaginary numbers are the idea of “rotating sideways”. Sometimes we find things in the real world that line up with the concept, so imaginary numbers are like moving North/South instead of East/West.
Can we have numbers in the 3rd dimension too?
- Yep! They’re the quaternions (technically 4d, and we can keep going higher). Eventually we use a matrix to keep track of the dimensions.
