Calculus Study Guide
To “Learn Calculus”, pick a goal below. This is an honest, realistic and self-motivating learning plan.
- Focus on bang for the buck: What’s the best way to spend 10 minutes? 2 hours?
- Explore analogies, diagrams, and examples before diving into the technical details.
- See learning as a progressive journey of discovery, not an all-or-nothing accomplishment.
Goal: Quick Insight (1 minute)
Calculus is the art of splitting patterns apart (X-rays, derivatives) and gluing patterns together (Time-lapses, integrals). Sometimes we can cleverly re-arrange the pattern to find a new insight.
A circle can be split into rings:
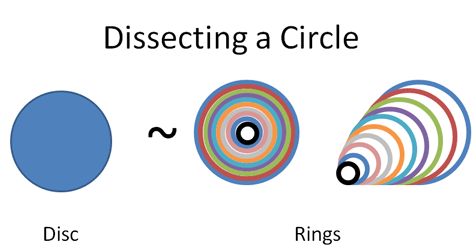
And the rings turned into a triangle:
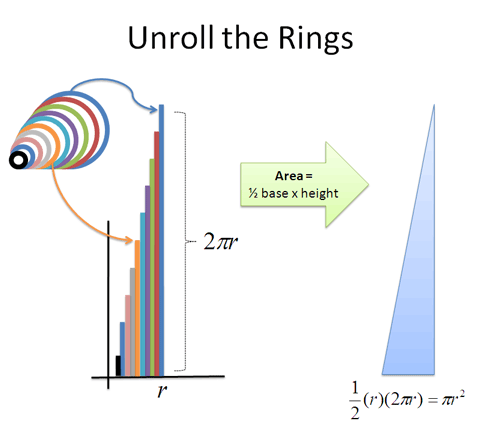
Wow! We found the circle’s area in a simpler way. Welcome to Calculus.
Checkpoint:
- Do you want to learn more more?
Goal: Intuitive Appreciation (30 mins)
Read:
- Lesson 1 - Use X-Ray and Time-Lapse Vision
- Lesson 2 - Practice Your X-Ray and Time-Lapse Vision
- Lesson 3 - Expanding Our Intuition
Checkpoint: Describe, in your own words:
- What Calculus does
- X-Ray Vision
- Time-lapse Vision
- The tradeoffs when splitting a circle into rings, wedges, or boards
- How to build a 3d shape from 2d parts
Goal: Technical Description (30 mins)
Read:
Checkpoint: Describe, in your own words:
- Integral
- Derivative
- Integrand (a single step)
- Bounds of integration
Skills:
- Describe a Calculus action (splitting a circle into rings) using the official language
- Enter the official language into Wolfram Alpha to solve the problem
Goal: Theory I (30 mins)
Read:
- Lesson 6 - Improving Arithmetic And Algebra
- Lesson 7 - Seeing How Lines Work
- Lesson 8 - Playing With Squares
Checkpoint: Describe, in your own words:
- How integrals/derivatives relate to multiplication/division
Skills:
- Find the derivative/integral of a line
- Find the derivative/integral of a constant
- Find the derivative/integral of a square
- Recognize the common notations for the derivative
- Estimate the change in $f(x) = x^2$ using a step of size $dx$
Goal: Theory II (1 hour)
Read:
- Lesson 9 - Working With Infinity
- Lesson 10 - The Theory Of Derivatives
- Lesson 11 - The Fundamental Theorem Of Calculus (FTOC)
- Lesson 12 - The Basic Arithmetic Of Calculus
- Lesson 13 - Finding Patterns In The Rules
- Lesson 14 - The Fancy Arithmetic Of Calculus
Checkpoint: Describe, in your own words:
- How an infinite process can have a finite result
- How a process with limited precision can point to a perfect result
- The formal definition of the derivative
- Estimate the change in $f(x) = x^2$ using a step of size $dx$, and let $dx$ go to zero. Verify the limit using Wolfram Alpha.
- The Fundamental Theorem of Calculus (FTOC)
Derive and put into your own words:
- The addition rule: $(f + g)’ = ?$
- The product rule: $(f * g)’ = ?$
- The inverse rule: $(\frac{1}{x})’ = ?$
- The power rule: $ (x^n)’ = ? $
- The quotient rule: $(\frac{f}{g})’ = ? $
- Solve $ \frac{d}{dx} 3x^5 $ on your own and verify with Wolfram Alpha
- Solve $ \int 2x^2 $ on your own and verify with Wolfram Alpha
Goal: Basic Problem Solving (1 hour)
Read:
Checkpoint: Describe how to turn the circumference of a circle into the area of a circle:
- Explain your plan in plain English
- Explain your plan using the official math notation
- Apply the rules of Calculus to your equation and calculate the result
- Verify the result using Wolfram Alpha
- Repeat the steps above, turning the area of a circle into the volume of a sphere
- Repeat the steps above, turning the volume of a sphere into the surface area of a sphere
Goal: Hey, I really need to pass this course! (12 weeks)
Gotcha. The best use of time is still spending a few hours on the above goals, to build a solid intuition. Then, begin your Calculus course, such as:
-
Elementary Calculus: An Infinitesimal Approach by Jerome Keisler (2002). This book is based on infinitesimals (an alternative to limits, which I like) and has plenty of practice problems. Available in print or free online.
-
Calculus Made Easy by Silvanus Thompson (1914). This book follows the traditional limit approach, and is written in a down-to-earth style. Available on Project Gutenberg and print.
-
MIT 1801: Single Variable Calculus. Includes video lectures, assignments, exams, and solutions. Available free online.
As you go through the traditional course, keep this in mind:
-
Review the intuitive definition. Rephrase technical definitions in terms that make sense to you.
-
It’s completely fine to use online tools for help. When stuck, get a hint, fix your mistakes, and try solving a new problem on your own.
-
Relate graphs back to shapes. Most courses emphasize graphs and slopes; convert the concepts to shapes to help visualize them.
-
Skip limits if you get stuck. Limits (and infinitesimals) were invented after the majority of Calculus. If you struggle, move on and return later.