Question: I was wondering if you have ever come across a nice explanation as to why equations such as “z + x + y = 0” are 2D planes?
My intuition is that equations have:
- variables (x, y, z) which are quantities that can change
- fixed values (0) which are quantities that must stay the same
Solving an equation means modifying the adjustable items (x, y, z) until they fit the “fixed” ones.
For example, x = 3 only has one solution (that x must be 3) in order to match the fixed value of 3.
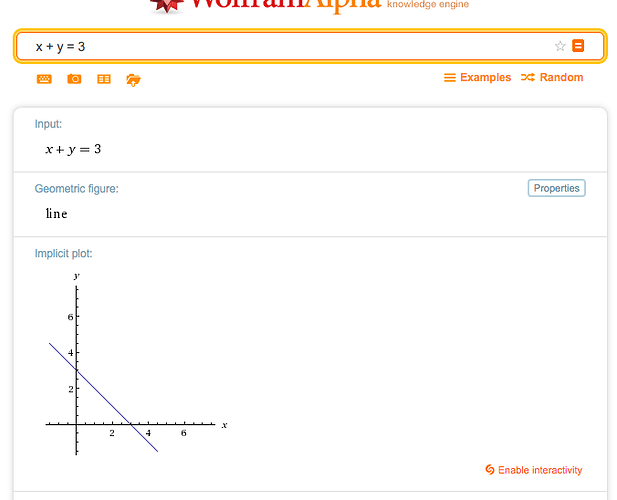
x + y = 3 has many solutions. We can adjust both x and y to meet the criteria (x =0 & y=3, x=1 & y=2). We can represent all these possibilities as a line:
The line represents all the solutions that work. What’s interesting is the solutions follow a 1-dimensional path (a straight line) but it’s embedded in the 2d grid. Basically, the grid shows all possibilities for x & y, and the line is a single path through that actually matches.
For a more advanced scenario like
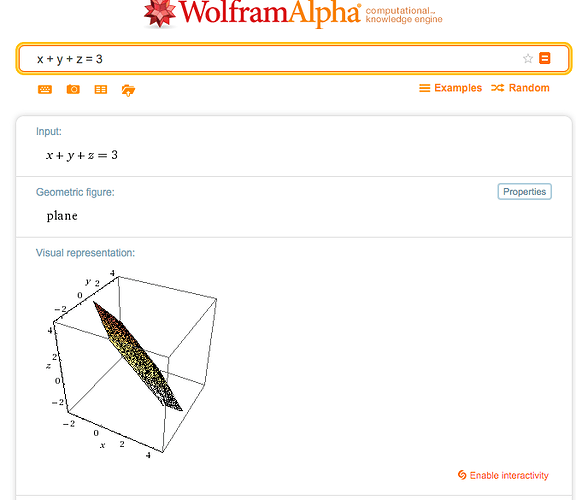
x + y + z = 3
we have 3 items which can move together (x =1, y=1, z=1, and so on). Now, these items aren’t truly independent: once we pick x and y, there’s only a single value of z that will work. In this way, we have 2 “degrees of freedom” embedded in a 3d set of possibilities:
A plane is basically lets us pick any x&y (length and width) in our space, and tells us the single z value (height) that we need to match the constraint.
We’re used to planes being perfectly vertical or horizontal, which makes it harder to visualize how a plane could be tilted. (Essentially, the tilt shows us what value of z is needed to meet the constraint.)