Quick tips on building a “BetterExplained-style” explanation.
1. Find a short analogy
What is the simplest distillation of the aha! moment? Examples: “Imaginary numbers are rotations” or “e is continuously compounded growth”.
2. Make a quick diagram
Can the analogy be visualized?
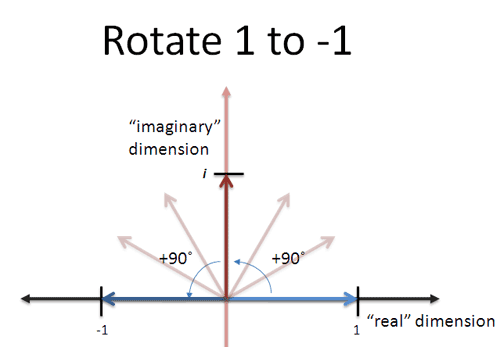
3. Work through an example based on the analogy
This could be a practice problem, or explaining the formal definition using the analogy.
If $i$ is a 90-degree rotation, then $i \cdot i$ should be a 180-degree rotation. And yes, $i^2 = -1$ . Similarly, $i^4$ should be a full rotation, or 1.We can also work through a rotation problem…
Template (ADEPT)
Analogy:
Diagram:
Example:
Principle (plain English):
Theory (formal description)
Imaginary Numbers
Fourier Transform
Euler’s Formula
Can go recursive as well (for one subelement of the idea, get the analogy, diagram, example).
Note: the analogy depth can be adjusted for your level. For example, can compare Vector Calculus to earlier Calculus concepts. Use the existing knowledge of your audience when possible.